Paper Summary

The paper ‘Glass Breaking in Fires’ by P. J. Pagni and A. A. Joshi builds on the authors’ earlier work  to ‘accurately’ predict the time of window breakage in compartment fires for any fire exposure.  In 1991 when the paper was published the literature and experimental work on this important problem were not well developed (Emmons).

Window breakage due to fire exposure has been determined to be due to differential heating between the field of the window and the unexposed edges in the frame.  As the field heats and expands the cooler edges are subjected to induced tensile stress.  When the imparted tensile stress exceeds the tensile strength of the glass it cracks.

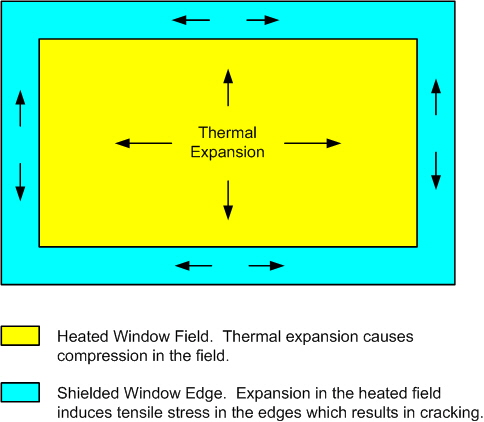
It should be noted that the material, physical and thermal properties of the frame (usually wood or metal) are of little consequence for ‘real’ compartment fires. The breakage mechanism requires only that the frame shields the edges of the glazing from radiant heat and hot gases.

Fire forensics (Kirk’s) tell us that window cracking from fire almost always initiates at the top edges of the window (initiating at defects which are often the result of cutting or poor handling) and spreads rapidly into the field with bifurcation.

‘Glass Breaking in Fires’ states simple strain criterion for glass temperature increase based on earlier work.  The paper then defines material properties for soda-lime glass and the geometry of the problem.

The exposed field of the window is assumed to be heated evenly on the compartment side by convection and radiation from the fire.  The radiative heat from the flame is distributed through the glass because of its relatively short wavelengths.  Otherwise the glass is treated as a gray body.  Heat is lost to ambient on the unexposed face through buoyant convection and radiation.

A partial differential equation is formulated for the time dependence of the temperature of the glass in the field as a function of distance through the glass.  A solution for the heat fluxes is solved analytically leading to a non-dimensional numerical solution for the governing equation.

The analysis proceeds with the analytical calculation of the two-dimensional time dependent temperature field through the thickness of the glazing on the horizontal window axis about the frame edge boundary.  The analytical solution is solved by numerical integration leading to a two-dimensional solution for the temperature field about the frame boundary.

An approximation to the normalized stress in the plane of the glazing is then calculated based on simple stress/strain relationships resulting from the strain due to the integral of the thermal expansion through the glass thickness.

By evaluating the temperature fields of ‘a large range’ of parameters the authors’ establish that at the time of breakage the mean temperature through the window about the frame edge can be approximated by a hyperbolic tangent.  This leads to an elegant simplification of the stress calculation based on a geometric factor which depends only on the width of the glazing shielded by the frame, the thickness the glazing and the width (height) of the exposed area of the window.

For practical windows the geometric factor, g, is approximately unity which leads to the following important conclusion:

Where the frame shading is large and the heating is fast the time to breakage
can be determined from the temperature history of the centre of the window.

In other cases the stress field must be specifically determined from the two dimensional temperature field in order to calculate when glazing exposed to a compartment fire is expected to break. The paper provides this calculation.